此博客为麻省理工学院公开课《微分方程》课程的复习笔记和博主个人的理解。

ODE 的几何解法： 方向场、积分曲线

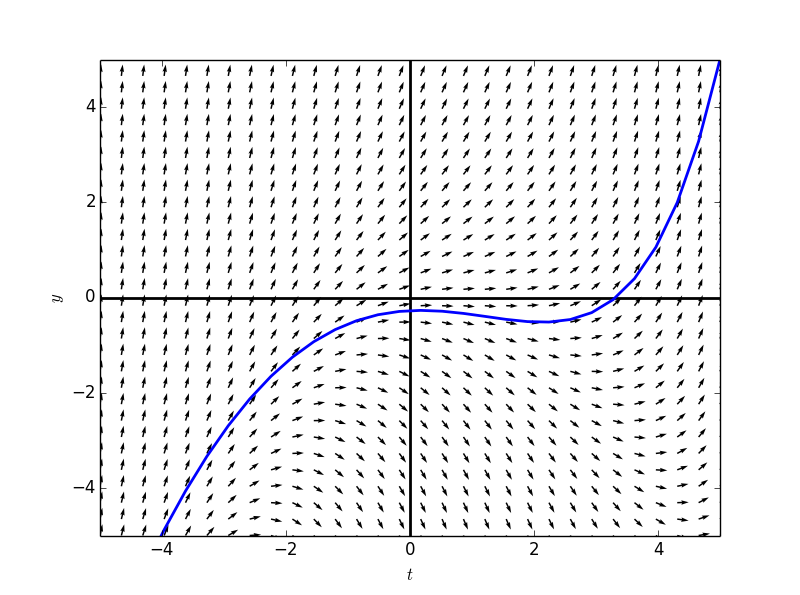
假设有微分方程： \begin{equation} f^\prime(x) = g(x, f(x)) \label{eq:ode_defin} \end{equation} 对于函数 $f(x)$ , 我们已经知道其导函数 $f^\prime(x)$ 的几何意义为函数上每一点的切线的斜率。 对于微分方程\eqref{eq:ode_defin}， 我们可以从中直观了解到的信息为函数 $f(x)$ 的斜率满足一个函数 $g(x, f(x))$ ， 但是对于这个函数 $f(x)$ 的解析表达式是不能直观看出来的， 但是我们可以肯定的是假如我们画出这个函数的曲线， 那么在曲线上的任意点 $(x_0, y_0)$ 上的切线的斜率肯定是 $g(x_0, y_0)$ 。 但是现在我们并不知道函数的具体曲线是什么， 但是有一点我们非常清楚， 那就是任意点的斜率我们都知道， 所以可以将平面中每一点的斜率都计算出来， 然后画出一个斜率图：

欧拉数值方法及推广

一阶线性常微分方程解法

一阶方程代换法

一阶自治微分方程

复数及复指数

一阶常系数线性方程

二阶常系数线性方程

二阶齐次线性方程

二阶非齐次方程

非齐次方程特解求法

共振

傅里叶级数简介

通过傅里叶级数求特解

拉普拉斯变换简介

拉普拉斯变换求线性常微分方程

卷积公式

利用拉普拉斯变换求解非连续输入 ODE

狄拉克 $\delta$ 函数

一阶常微分方程组

常系数齐次线性方程组

2X2 齐次线性方程组作图

非齐次方程组矩阵方法

矩阵指数

常系数解耦线性方程组

非线性自治系统

极限环

非线性方程组和一阶常微分方程之间的关联

欢迎加入 scala 成都技术交流群